Big O Notation.

Big notation is a way for you to describe how the time it takes for your function to run grows in respect to the size of the input of said function.

If you have a function that runs a loop to add a set of numbers in an array, one question one might ask is how many milliseconds it takes to run the function. This is very difficult to answer since speed of code depends on a number of different factors that are mostly not under your control. So an easier question to ask would be “how does the time it takes to run this function grow in respect to the size of the array?”

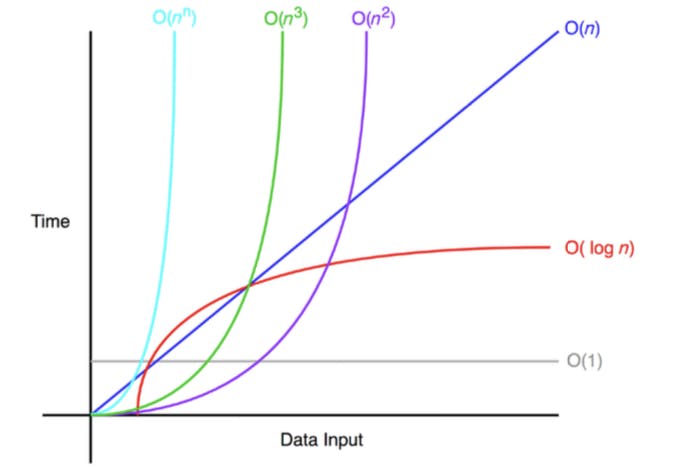
Types of time complexities

There are different types of time complexities:

1. Constant time complexity
2. Linear time complexity
3. Quadratic time complexity
4. Cubic time complexity
5. Logarithmic time complexity

The image below is a graphical representation of algorithms with the big O notations of the above mentioned time complexities.

Constant time complexity (O(1))

An example of an algorithm with constant time is one that performs only a single operation on an array of n length. Eg,

1. Algorithm to return the first element of the array.
2. Algorithm to return the last element of the array
3. Algorithm to return an element at a specified index.

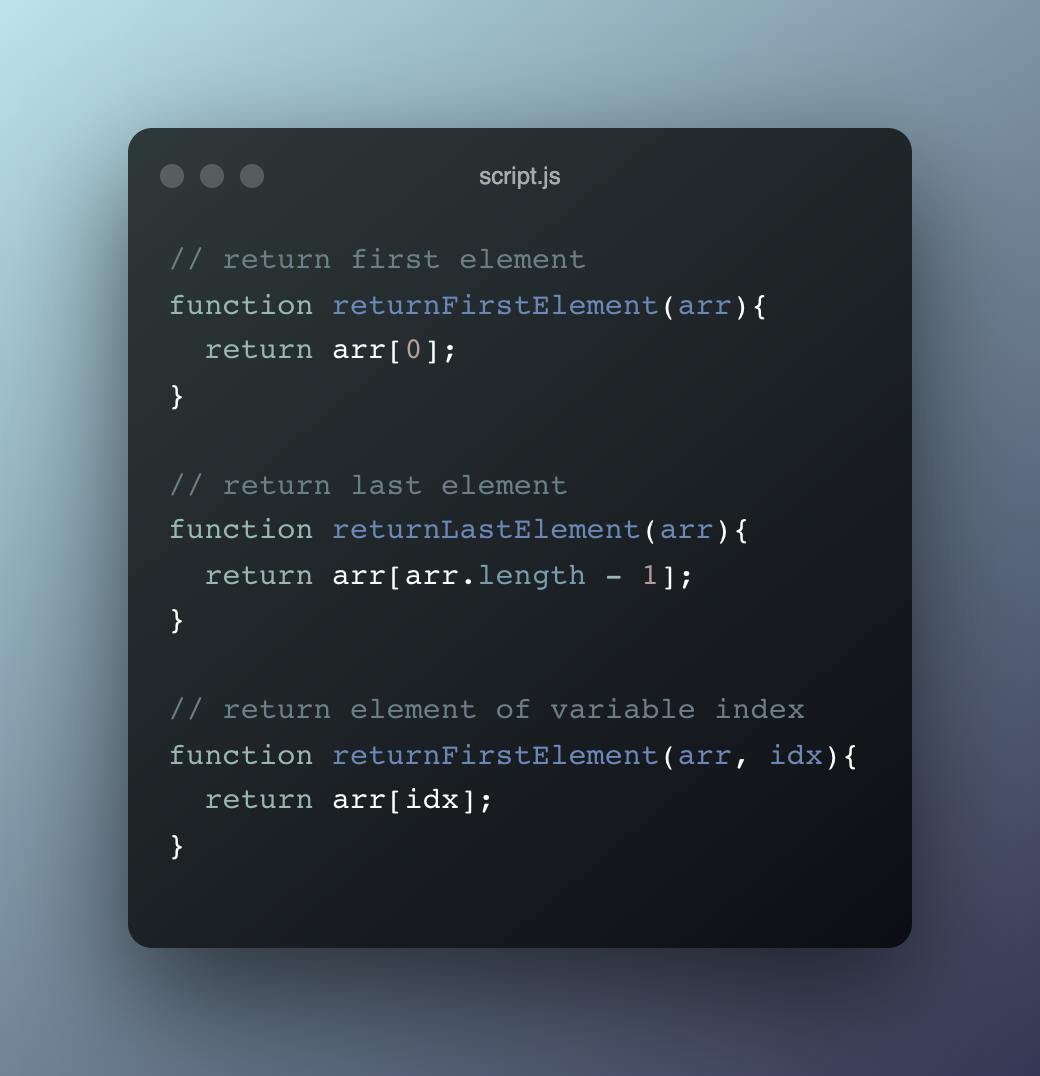
The big O notation of such an algorithm would be O(1). It’s called constant because the size of the array doesn’t increase the time it takes to get the first or last element of the array.

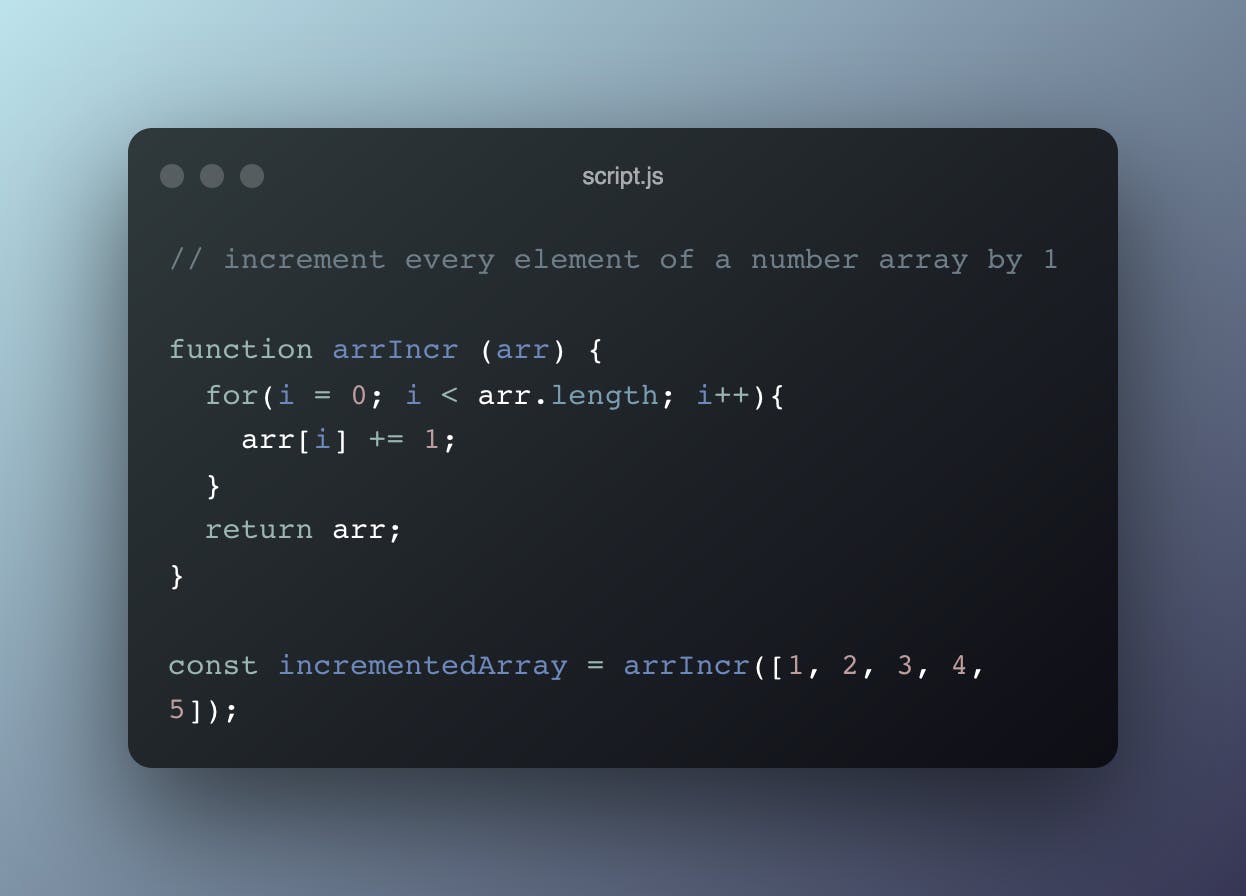
Linear time complexity (O(n))

With algorithms of linear time complexities, the time taken to run the algorithm is directly proportional to the size of the array such that the time it takes increases directly as the size increases. This usually describes an algorithm with a single operation, probably, to increase each element of a number array by 1. The big O notation of such an algorithm would be O(n).

Quadratic time complexity

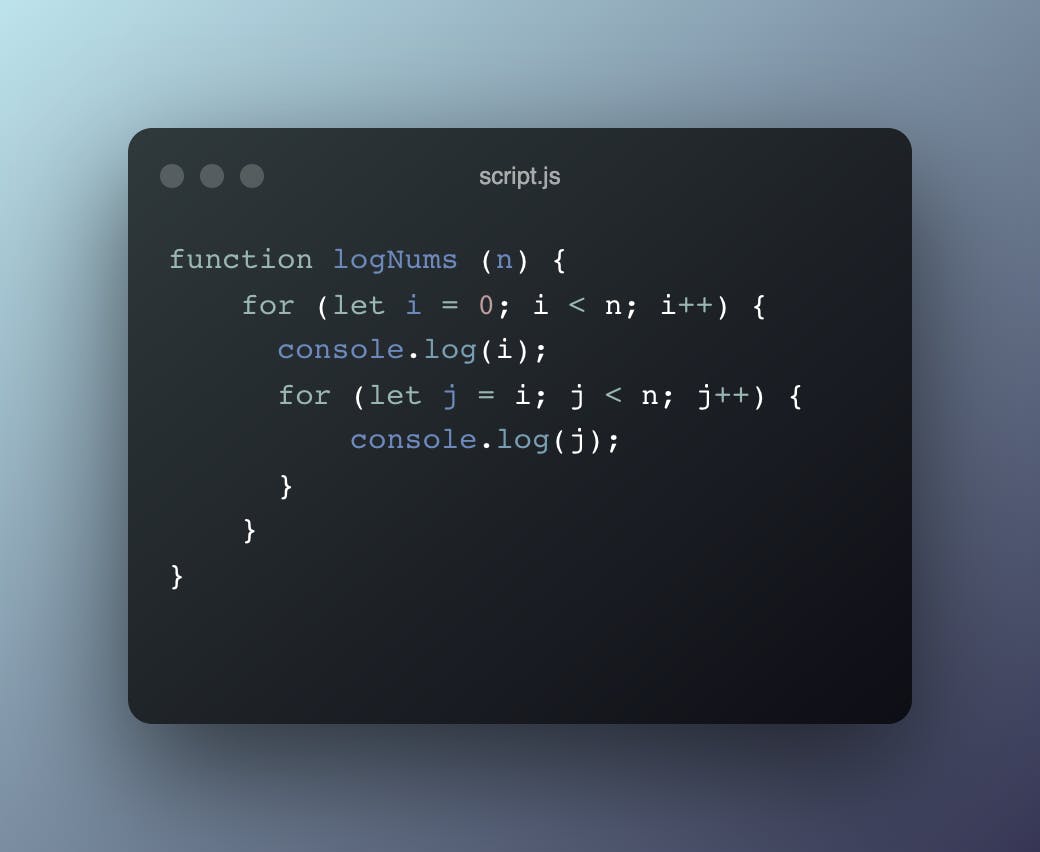
An algorithm of quadratic time complexity would be described as one whose time increases exponentially as the size of the array increases. An example of such algorithm would be one with two nested loops where the time taken to run the inner loop increases as you go further towards the index of the last element of the array. The big O notation of such an algorithm would be O(n^2).

For example:

Cubic time complexity

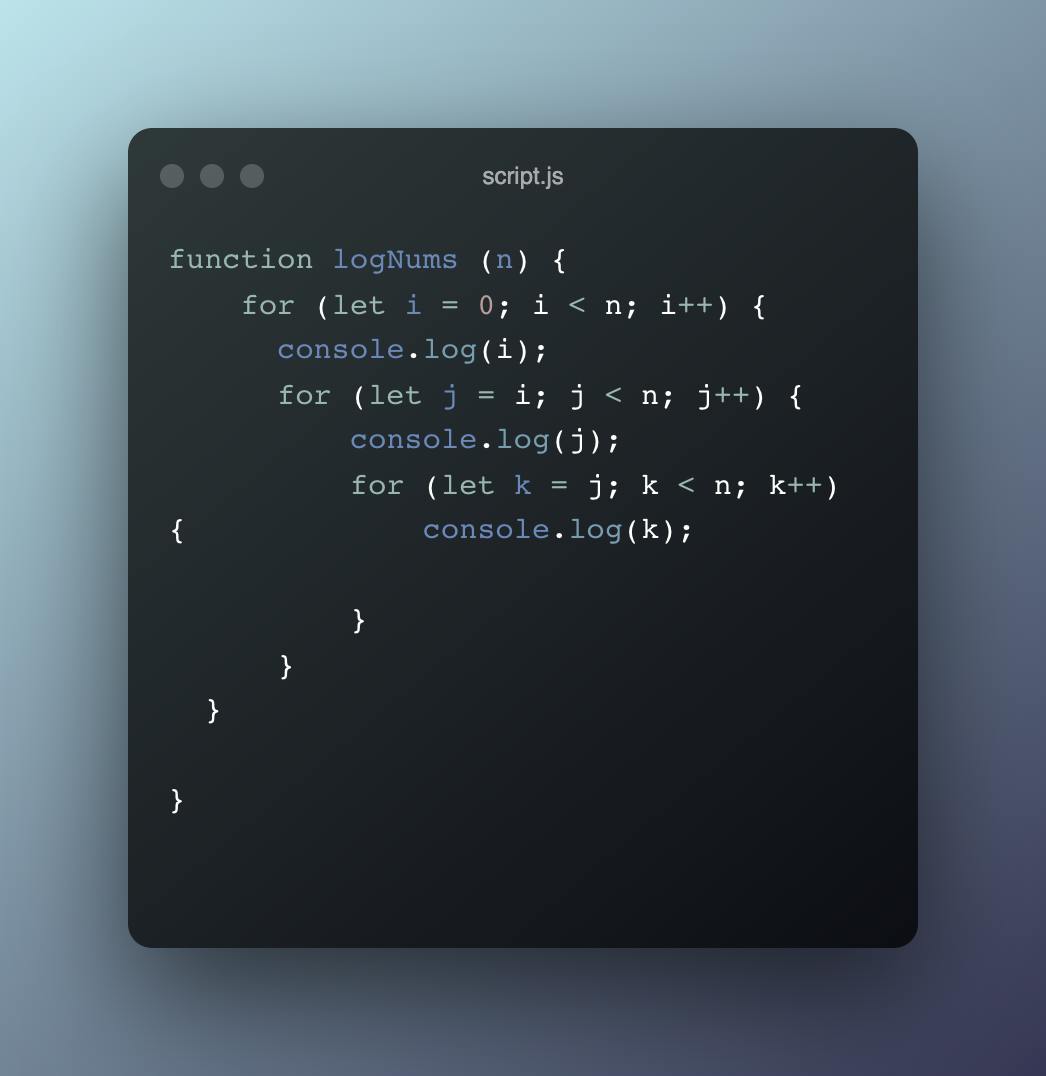
An algorithm of cubic time complexity would as well be described as one whose time increases exponentially as the size of the array increases but to a higher degree than the quadratic. An example of such algorithm would be one with three nested loops where the time taken to run each level of the nesting increases exponentially as you go further towards the index of the last element of the array. The big o notation of such an algorithm would be O(n^3)

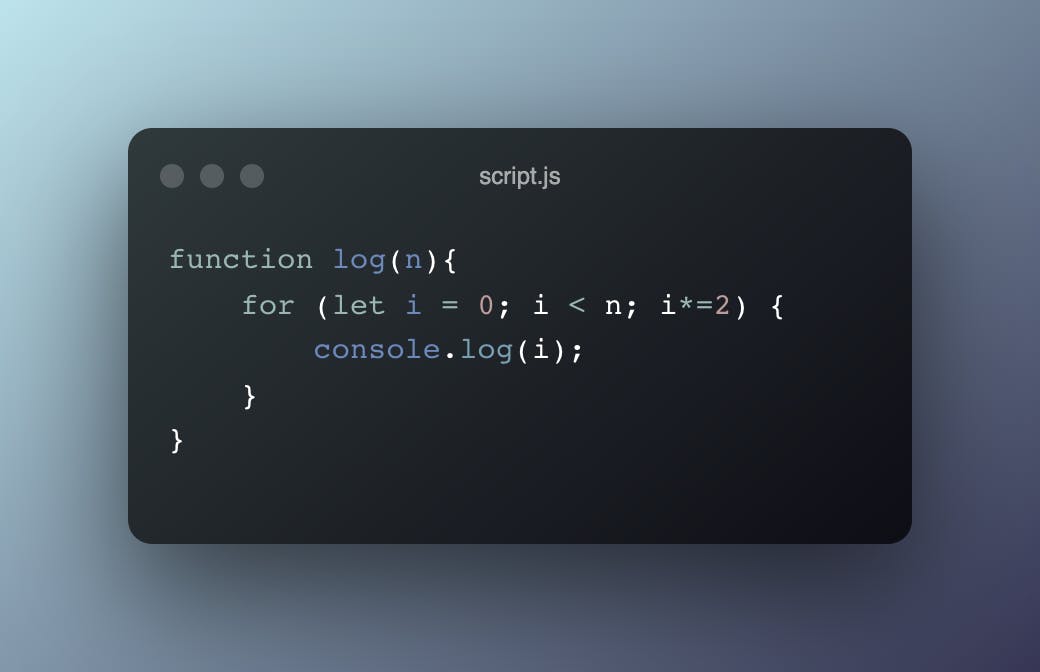
Logarithmic time complexity

Mathematically, "logarithm" refers to the power a number needs to be raise to to give a certain number. example, Logx (base a)=y means a ^ y = x. Logarithmic time complexities are usually based on certain values. For example;

Rules of big O notation.

1. Coefficient rule: if there is a function f(n) with a big o notation of O(n), k*f(n) would remain O(n) for every constant k > 0.

2. Sum rule: if there is a function f(n) with a big O notation of O(a(n)) and another function g(n) with a big O notation of O(b(n)), the big O notation of f(n) + g(n) would be O(a(n) + b(n)).

3. Product rule: if there is a function f(n) with a big O notation of O(a(n)) and another function g(n) with a big O notation of O(b(n)), the big O notation of f(n) g(n) would be O(a(n) b(n)).

4. Transitive rule: if there is a function f(n) with a big O notation of O(g(n)) and the big O notation of the function g(n) is O(h(n)) then this implies that the big O notation of f(n) can be described as O(h(n)).

5. Polynomial rule: if there is a polynomial function f(n) with a degree of k, the big O notation of f(n) is O(n^k).

6. Log of a power rule: if there is a logarithmic function log(n*k), the big O notation of such function is O(log(n)) given any constant k > 0.